COSTRUZIONI GEOMETRICHE 4: bisettrice di un angolo

Definizione: la bisettrice di un angolo è la semiretta con origine nel vertice e che divide l'angolo in due parti uguali.


Svolgimento
Per costruire la bisettrice di un angolo utilizziamo la proprietà di cui godono tutti e solo i suoi punti, cioè di essere equidistanti dai lati dell'angolo.

Per effettuare la costruzione si inizia col tracciare due semirette aventi la stessa origine V. Su una di queste si sceglie un punto qualsiasi A.

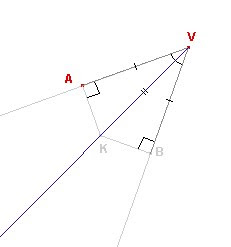
Si riporta con il compasso, puntato in V, la misura del segmento AV sull'altro lato dell'angolo in modo tale che VA = VB. Dal punto B si tracciano la retta perpendicolare al lato VB dell'angolo, e la perpendicolare per A alla semiretta VA. L'incontro di tali perpendicolari individua il punto K. Poiché due triangoli rettangoli sono congruenti se hanno rispettivamente uguali l'ipotenusa ed un cateto, ne segue che AK = BK. Allora K è equidistante dai due lati dell'angolo. Si traccia infine la semiretta che unisce i punti K e V : tale semiretta è la bisettrice. Questa contiene tutti e soli i punti equidistanti dai lati dell'angolo.

Definizione: le tre bisettrici degli angoli interni di un triangolo si incontrano in uno stesso punto chiamato incentro.