COSTRUZIONI GEOMETRICHE 9: punti notevoli di un triangolo

 Definizione 1: il baricentro di un triangolo è il punto di incontro delle tre mediane.
Definizione 2: il circocentro di un triangolo è il punto di incontro dei tre assi.
Definizione 3: l'incentro di un triangolo è il punto di incontro delle tre bisettrici.

Definizione 4: la mediana di un triangolo relativa ad un lato è il segmento che ha per estremi un vertice ed il punto medio del lato opposto.


Costruzione geometrica 1

Disegnare un triangolo scaleno.
Ora tracciamo le tre mediane unendo ogni vertice del triangolo con il punto medio del lato opposto.
Nota che le mediane del triangolo passano tutte per lo stesso punto, il baricentro, e che tale punto è sempre interno al triangolo.

Proprietà del baricentro: il baricentro divide ogni mediana in due parti in cui quella che ha un estremo nel vertice è doppia dell'altra.

Costruzione geometrica 2

Disegnare un triangolo scaleno.
Per costruire il circocentro di un triangolo qualsiasi ABC, dobbiamo tracciare gli assi di almeno due lati del triangolo.
Ricordiamoci che l'asse di un segmento è il luogo dei punti equidistante dagli estremi del segmento. L'asse di un segmento passa per il punto medio ed è perpendicolare al segmento.

Il circocentro di un triangolo è il punto equidistante dai suoi vertici. E' quindi anche il centro della circonferenza circoscritta. Da qui il nome circocentro.

Costruzione geometrica 3

Disegnare un triangolo scaleno.
Per costruire l'incentro di un triangolo qualsiasi ABC, dobbiamo tracciare la bisettrice di almeno due angoli del triangolo.

Ricordiamoci che la bisettrice di un angolo è il luogo geometrico dei punti del piano equidistante dai lati dell'angolo. Questo si traduce nel fatto che la bisettrice di un angolo è una semiretta che divide l'angolo in due parti uguali.

L'intersezione di tali bisettrice è il punto chiamato incentro. Il nome incentro deriva dalla proprietà dell'incentro, e da cui deriva il suo nome, è quella di essere il centro della circonferenza inscritta al triangolo.

Attività: prova a verificare se l'incentro,circocentro e baricentro del triangolo sono punti sempre interni al triangolo, oppure possono essere esterni.

COSTRUZIONI GEOMETRICHE 8: costruire un esagono regolare

Definizione: si dice  regolare un poligono equilatero ed equiangolo.

Teorema: il lato dell'esagono regolare è uguale al raggio della circonferenza circoscritta.


Costruzione geometrica
Vogliamo costruire un esagono regolare di lato AB assegnato.

Poiché è valido il precedente teorema si può operare come segue:

•    Tracciamo una circonferenza di raggio OA
•    scelto un punto qualsiasi A su questa circonferenza, fatto centro in A e raggio uguale ad OA tracciamo una nuova circonferenza che interseca la prima in due punti B ed F
•    il segmento AB, lato dell'esagono, è dunque uguale al raggio della circonferenza.
•    facendo centro in B tracciamo ora la circonferenza di raggio AB, determiniamo il nuovo punto intersezione C;
•    ripetiamo la costruzione in modo da determinare i punti d'intersezione D, E;
•    disegniamo i segmenti BC, CD, DE, EF, FA che costitutiscono i lati dell'esagono.


Proprietà: ogni angolo interno di un esagono regolare misura 120°, questo perchè l'esagono può essere suddiviso in 6 triangoli equilateri per cui.......

Nota: se volete vedere tuttala costruzione seguite il link: http://www.math.it/cabri/esagono.htm
Potete anche vedere la costruzione dell'ottagono: http://www.math.it/cabri/ottagono.htm

Giorno del pi greco

Il giorno dedicato al pi greco è il 14 marzo: la scelta è stata ispirata dalla scrittura anglosassone per questo giorno, 3.14, scrittura che richiama l'approssimazione con tre cifre di pi greco. Qualcuno si sforza di celebrare il famoso numero trascendente esattamente alle 1:59 del pomeriggio, in modo di adeguarsi alla approssimazione con sei cifre 3.14159.
La prima celebrazione in occasione del "Pi Day" si tenne nel 1988 all'Exploratorium di San Francisco, per iniziativa del fisico americano Larry Shaw, in seguito insignito del titolo di "Principe del pi greco". Il calendario della prima manifestazione prevedeva un corteo circolare attorno ad uno degli edifici del museo e la vendita di torte alla frutta, decorate con le cifre decimali del pi greco.
In questi giorni nei dipartimenti di matematica in varie istituzioni nel mondo si coglie l'occasione per organizzare delle feste. La celebrazione avviene anche in comunità virtuali come Second Life e Facebook.
Il 14 marzo 2010 Google ha omaggiato la giornata del pi greco con una versione artistica del proprio logo

Giorno dell'approssimazione di pi greco

Il giorno dell'approssimazione di pi greco può ricorrere in una delle seguenti date.

• 22 luglio: 22/7 è un'approssimazione di π nota fin dai tempi di Archimede.
• 26 aprile (o 25 aprile negli anni bisestili): per tale data, partendo dal 1º gennaio, la Terra percorre un arco di circonferenza pari a 2 radianti, equivalente a 1⁄π volte l'orbita totale intorno al Sole. L'istante esatto in cui ciò accade è alle 04:23:41 del 26 aprile, 116º giorno dell'anno. Negli anni bisestili, l'istante esatto è alle 12:02:03 del 25 aprile, 116º giorno dell'anno.
• 10 novembre (9 novembre negli anni bisestili): 314º giorno dell'anno in base al calendario gregoriano.
• 21 dicembre (20 dicembre negli anni bisestili): 355º giorno dell'anno, all'1:13 pm, coincidente con il valore approssimato di 355/113 dovuto al matematico cinese Zu Chongzhi.

(articolo tratto da:   http://it.wikipedia.org/wiki/Giorno_di_pi_greco)

Problema 3.5: i tre candidati di Roncofritto

Ci sono 3 candidati alle elezioni di "Roncofritto", un piccolo paesino di 40 anime (candidati compresi...).
Qual'è il numero minimo di voti che deve ricevere il candidato per vincere le elezioni?

(Problema posto da Fabiana S. 1Al)

Problema 3.4: le mele di Pinco e Pallino

Pinco e Pallino hanno delle mele. Se Pinco ne da una a Pallino, ne avrebbero la stessa quantità; se Pallino ne da 2 a Pinco, questi ne avrebbe il triplo di Pallino.
Quante mele ha ciascuno?
(Problema suggerito da Fabiana S. 1Al)

Problema 3.3: costruzione senza matite

Sapresti costruire quattro quadratini identici muovendo solo due fiammiferi?

Problema 3.2*: il gioco dei sacchetti

Ci sono due sacchetti, rispettivamente con 12 e 7 gettoni. Due giocatori, a turno, buttano via i gettoni di un sacchetto a loro scelta e ripartiscono i gettoni dell’altro nei due sacchetti. Perde chi si trova nella situazione in cui ciascuno dei due sacchetti contiene 1 gettone (e quindi non può proseguire). C’è una strategia vincente per il giocatore che fa la prima mossa?

[Suggerimento. Attenzione ai numeri pari e ai numeri dispari. Una posizione è sicura se entrambi i sacchetti contengono un numero ……. di gettoni. Infatti, se lasciamo una posizione di questo tipo, il nostro avversario dovrà ridarci un sacchetto con un numero …… di gettoni e l’altro con un numero …… di gettoni. Noi, allora, …]

Problema 3.1: l’età dei tre figli

Due amici, amanti dei giochi matematici, si incontrano dopo diversi anni e cominciano a conversare finché il discorso va a finire sui figli.

A- “Che età hanno i tuoi tre figli?”
B- “Il prodotto delle loro età è uguale a 36”
A- “Dammi qualche altra informazione, questa non mi basta!”
B- “Hai ragione!La somma delle loro tre età è uguale al numero civico di quella casa”
A- “Non mi è sufficiente per dirti le loro età”
B- “Ti posso dire che il più piccolo ha gli occhi azzurri”
A-“Complimenti!”

Qual è l’età dei tre figli?

Problema 2.3*: gioco dei 21 stecchini

Ci sono 21 stecchini sul tavolo. A turno, ciascuno dei due giocatori toglie da 1 a 5 stecchini. Chi prende l’ultimo stecchino perde. C’è una strategia vincente per il giocatore che fa la prima mossa?

[Suggerimento. Occorre trovare quali sono le “posizioni sicure”, cioè le posizioni che assicurano la vittoria a chi le lascia all’avversario. Le posizioni sicure devono essere tali che:
• se la posizione è sicura, qualunque mossa la rende non sicura,
• se la posizione non è sicura, esiste una mossa che la rende sicura. ]

Problema 2.2: la foglia magica

Esiste una foglia che in un giorno cresce tanto da diventare il doppio del giorno precedente. Posta su un lago la foglia riesce a ricoprirlo in 30 giorni. Dopo quanti giorni ricopre la metà del lago?

Problema 2.1: i quattro triangoli

Avendo a disposizione sei fiammiferi, costruire quattro triangoli equilateri aventi per lato un intero fiammifero.

COSTRUZIONI GEOMETRICHE 7: dividere un segmento in parti uguali

Teorema di Talete: un fascio di rette parallele tagliate da due trasversali stacca su queste coppie di segmenti direttamente proporzionali.


Costruzione geometrica
Per dividere un segmento assegnato in n parti uguali, si procede come segue.

Scegliamo di dividere il segmento assegnato AB in 5 parti uguali.
- disegniamo il segmento AB;
- sulla semiretta di origine A segnamo un punto qualsiasi: chiamiamolo 1;
- riportiamo la lunghezza del segmento A-1 con lo strumento compasso facendo centro nel punto 1. Si individua così il punto 2;
- iteriamo il procedimento in modo da individuare sulla semiretta i punti 3, 4, 5 tutti equidistanti tra loro;
- tracciamo ora il segmento che unisce il punto 5 con l'estremo B;
- tracciamo le rette parallele al segmento 5-B passanti per i punti 4, 3, 2, 1.

Il segmento AB risulta in tal modo suddiviso in 5 segmenti uguali.

COSTRUZIONI GEOMETRICHE 6: teorema di TALETE

Teorema di Talete: un fascio di rette parallele tagliate da due trasversali stacca su queste coppie di segmenti direttamente proporzionali.


Costruzione geometrica
- disegniamo una retta r1 passante per un punto qualsiasi del piano
- tracciamo due qualsiasi rette parallele ad r1. Chiamiamole r2 ed r3
- l'insieme delle tre rette costituisce un fascio di rette parallele

- disegniamo ora due rette s ed s' trasversali (ovvero che tagliano il fascio di rette)
- detti P1, P2 e P3 i punti di intersezione di s con il fascio, e P'1, P'2 e P'3 i punti di intersezione di s',
- determiniamo sulle due rette le coppie di segmenti P1P2 , P2P3 e P'1P'2 , P'2P'3.

Come è possibile verificare:
- se variamo l'inclinazione di una retta, s o s', il rapporto tra i segmenti staccati su quella retta rimane costante: le grandezze dei due segmenti sono direttamente proporzionali
- i rapporti tra le due coppie di segmenti rimangono uguali tra loro al variare delle posizioni delle rette. Possiamo allora scrivere la proporzione:


P1P2 : P2P3 = P'1P'2 : P'2P'3

COSTRUZIONI GEOMETRICHE 5: rette perpendicolari e parallele

Problema 1: costruire la perpendicolare ad una retta data per un punto ad essa esterno.


Svolgimento
Per effettuare la costruzione esegui i seguenti passi:
- traccia una retta r ed un punto P del piano non appartenente ad r,
- con centro nel punto P traccia la circonferenza di raggio a piacere purché intersechi la retta r,
- su questa retta segna le due intersezioni M e N,
- traccia la circonferenza con centro M e raggio MP, e la circonferenza di centro N e raggio NP,
- segna il punto Q in cui si intersecano, (nota che Q è il simmetrico di P rispetto all'asse r),
- taccia la retta passante per P e per Q. Tale retta risulta perpendicolare ad r e passante per P.

Attività: prova a costruire la perpendicolare nel caso in cui P appartiene ad r.

 

Problema 2: costruire la parallela ad una retta per un punto ad essa esterno.



Svolgimento
- traccia una retta r ed un punto P non appartenente ad r,
- segna a tuo piacere un punto A sulla retta r,
- con centro nel punto P traccia la circonferenza di raggio PA,
- segna il punto B intersezione della circonferenza con r,
- con centro in B traccia la circonferenza di raggio BA,
- indica con C il punto di intersezione tra le due circonferenze; nota che i segmenti PA, PC, AB, BC sono tra loro uguali,
- la retta passante per P e C è parallela ad r.

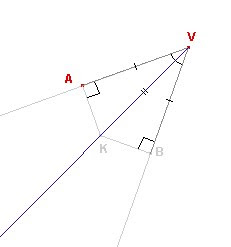
COSTRUZIONI GEOMETRICHE 4: bisettrice di un angolo

Definizione: la bisettrice di un angolo è la semiretta con origine nel vertice e che divide l'angolo in due parti uguali.


Svolgimento
Per costruire la bisettrice di un angolo utilizziamo la proprietà di cui godono tutti e solo i suoi punti, cioè di essere equidistanti dai lati dell'angolo.

Per effettuare la costruzione si inizia col tracciare due semirette aventi la stessa origine V. Su una di queste si sceglie un punto qualsiasi A.

Si riporta con il compasso, puntato in V, la misura del segmento AV sull'altro lato dell'angolo in modo tale che VA = VB. Dal punto B si tracciano la retta perpendicolare al lato VB dell'angolo, e la perpendicolare per A alla semiretta VA. L'incontro di tali perpendicolari individua il punto K. Poiché due triangoli rettangoli sono congruenti se hanno rispettivamente uguali l'ipotenusa ed un cateto, ne segue che AK = BK. Allora K è equidistante dai due lati dell'angolo. Si traccia infine la semiretta che unisce i punti K e V : tale semiretta è la bisettrice. Questa contiene tutti e soli i punti equidistanti dai lati dell'angolo.

Definizione: le tre bisettrici degli angoli interni di un triangolo si incontrano in uno stesso punto chiamato incentro.

COSTRUZIONI GEOMETRICHE 3: trasporto di un angolo

Problema: costruire un angolo uguale ad un angolo dato e avente per lato una prefissata semiretta (trasporto di una angolo).

Svolgimento
Supponiamo che siano stati assegnati un angolo AOB ed un segmento MN appartenente alla semiretta di origine M.
Per riportare l'angolo dato sulla semiretta esegui i seguenti passi:
1) Disegna un segmento di estremi A e B
2) Disegna un segmento più lungo di AB con estremi M ed N
3) Traccia una circonferenza di centro O e raggio OA; su questa circonferenza prendi un punto B
4) Traccia il segmento OB : l’angolo da trasportare è costruito!
5) Traccia una circonferenza di centro A e raggio OA,
6) Con centro in M traccia una circonferenza di raggio OA (usa lo strumento “Compasso”), chiama Q l'intersezione della circonferenza con il segmento MN
7) Traccia con centro in A una circonferenza di raggio AB,
8) Rripeti costruendo la circonferenza di centro Q e raggio AB (sempre usando lo strumento “Compasso”)
9) Le due circonferenze si incontrano in due punti, chiama R uno di questi
10) Unisci con un segmento i punti M ed R.
11) L'angolo NMR è l'angolo riportato uguale all'angolo dato.

COSTRUZIONI GEOMETRICHE 2: asse di un segmento

Definizione: l'asse di un segmento è la perpendicolare al segmento, condotta dal suo punto medio.
Teorema: l'asse di un segmento è il luogo geometrico dei punti del piano equidistanti dagli estremi del segmento.

Infatti per costruire l'asse di un segmento si traccia una circonferenza con il centro in un estremo del segmento, e che abbia il raggio di una misura qualsiasi purché più grande della metà del segmento. Poi, mantenendo la stessa apertura del compasso, si ripete la costruzione centrando una circonferenza nell'altro estremo. La retta che unisce i punti d'intersezione delle due circonferenze è l'asse del segmento.

Nota che tale retta passa per il punto medio del segmento. Infatti tale punto gode anch'esso della proprietà di appartenere al segmento e di essere equidistante dagli estremi del segmento.
Da tale costruzione puoi osservare che l'asse di un segmento passa per il punto medio ed è perpendicolare al segmento.

Gli assi di un triangolo si incontrano in uno stesso punto: il circocentro.

Anche i matematici hanno un cuore

Cari studenti,
in occasione della festa di San Valentino, volevo farvi vedere che anche i matematici hanno un cuore...

 

Vi piace questa funzione disegnata in 3d?  :)